Leo Zhou

Leo Zhou

Seeking truths in the quantum realm

My current research interests include:

  • developing quantum algorithms for classically hard problems;
  • exploring fundamental aspects of quantum physical systems from computational and complexity-theoretic perspectives;
  • finding practical applications of near-term quantum devices.
Below, I will briefly describe some research topics I have worked on in the past, along with related publications.

Complexity of Quantum Many-body Systems

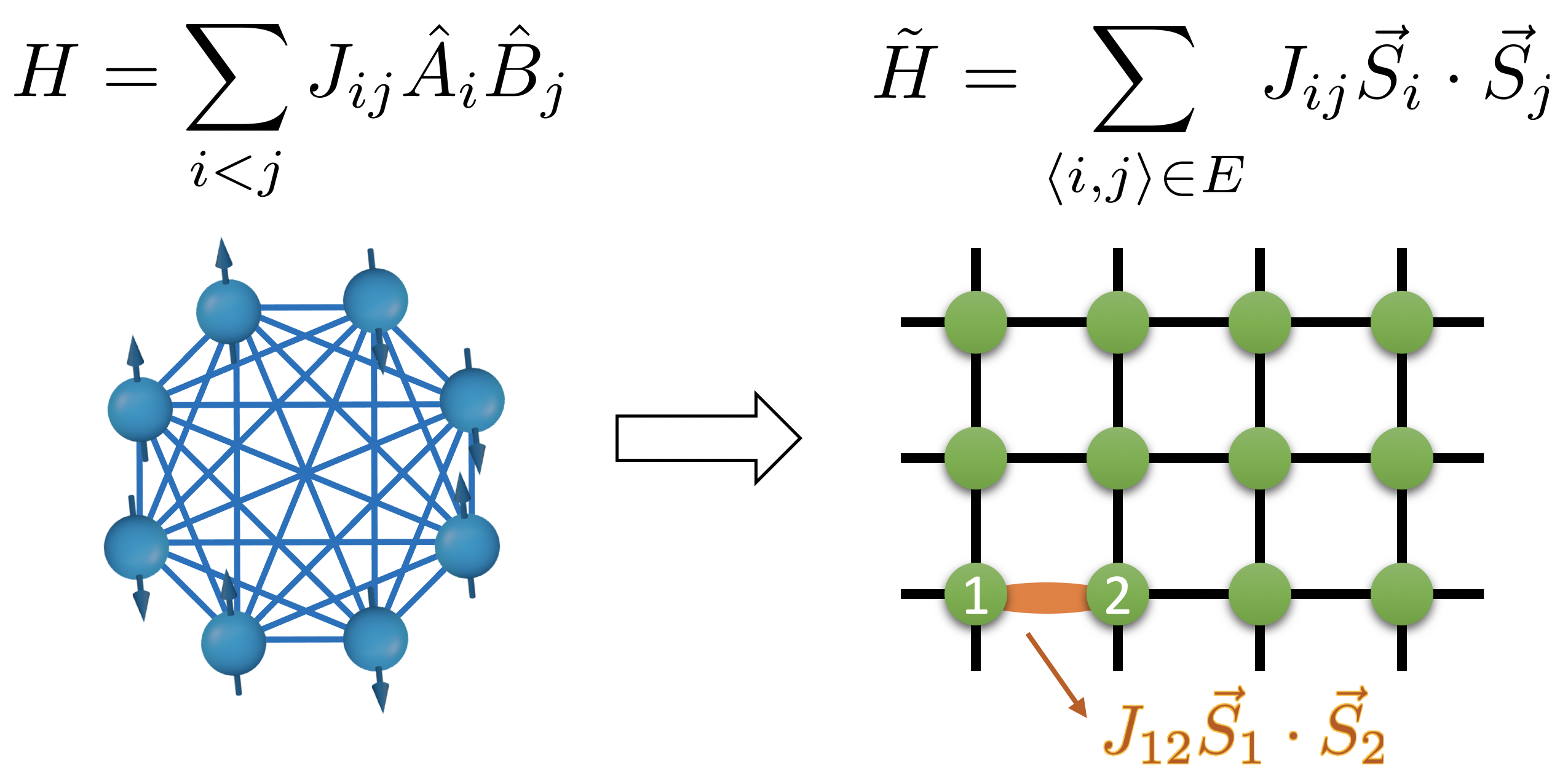Analog Hamiltonian simulation A system of many quantum particles is highly complex. Because of quantum entanglement, complete characterization of the state of a quantum system requires an exponentially large classical description in general. This nonclassicality necessitates developments of quantum extensions to classical complexity theory. For example, we can prove that some procedures that are often used in classical computer science for simplifying complex systems fundamentally cannot be generalized to the quantum setting. Another interesting question is: When can complex quantum systems be simulated by simpler ones? We show that certain simple 1D and 2D systems are universal simulators, in the sense that they can efficiently reproduce the physics of any physically realizable quantum systems. Furthermore, we develop theories to understand the energy landscape of quantum many-body system. Our results show that finding a local minimum of the energy is computational hard for classical computers, but easy for quantum computers.

Theory of Quantum Optimization Algorithms

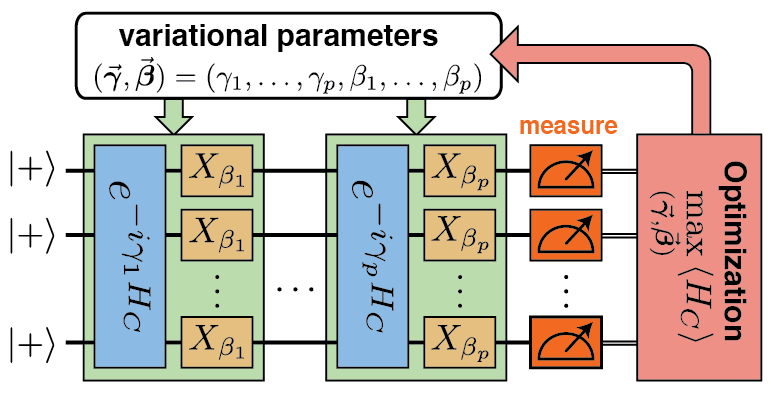QAOA circuit Since optimization problems are ubiquitous in real-world applications, it is important to understand whether there is any advantage in using quantum algorithms for solving them. Although a few quantum optimization algorithms have been proposed, we have very limited (and often merely heuristical) understanding of how well they work in practice. To address this issue, we perform both rigorous theoretical analysis and numerical experiments on the popular Quantum Approximate Optimization Algorithm (QAOA), which has seen small-scale implementations on current quantum devices. Our results show both provable advantages and limitations of the QAOA in the constant-depth regime, and shed light on physical mechanisms that suggest larger speedups at high depths. Furthermore, this line of research reveals many fruitful connections to the mathematical theory of spin glasses and high-dimensional statistics. A provocative open question is: Can quantum algorithms achieve superpolynomial quantum speedups in optimization problems? This could be achieved, for example, by overcoming (provable) barriers well-studied in classical algorithms such as the overlap gap property (OGP).

  • Performance and limitations of the QAOA at constant levels on large sparse hypergraphs and spin glass models [FOCS 2022] (video)
  • The QAOA at High Depth for MaxCut on Large-Girth Regular Graphs and the Sherrington-Kirkpatrick Model [TQC 2022, Outstanding Paper Award] (video)
  • The Quantum Approximate Optimization Algorithm and the Sherrington-Kirkpatrick Model at Infinite Size [QIP 2021; Quantum (2022)] (video)
  • Quantum Approximate Optimization Algorithm: Performance, Mechanism, and Implementation on Near-Term Devices [Phys. Rev. X (2020)]

Experimental Realizations of Quantum Applications

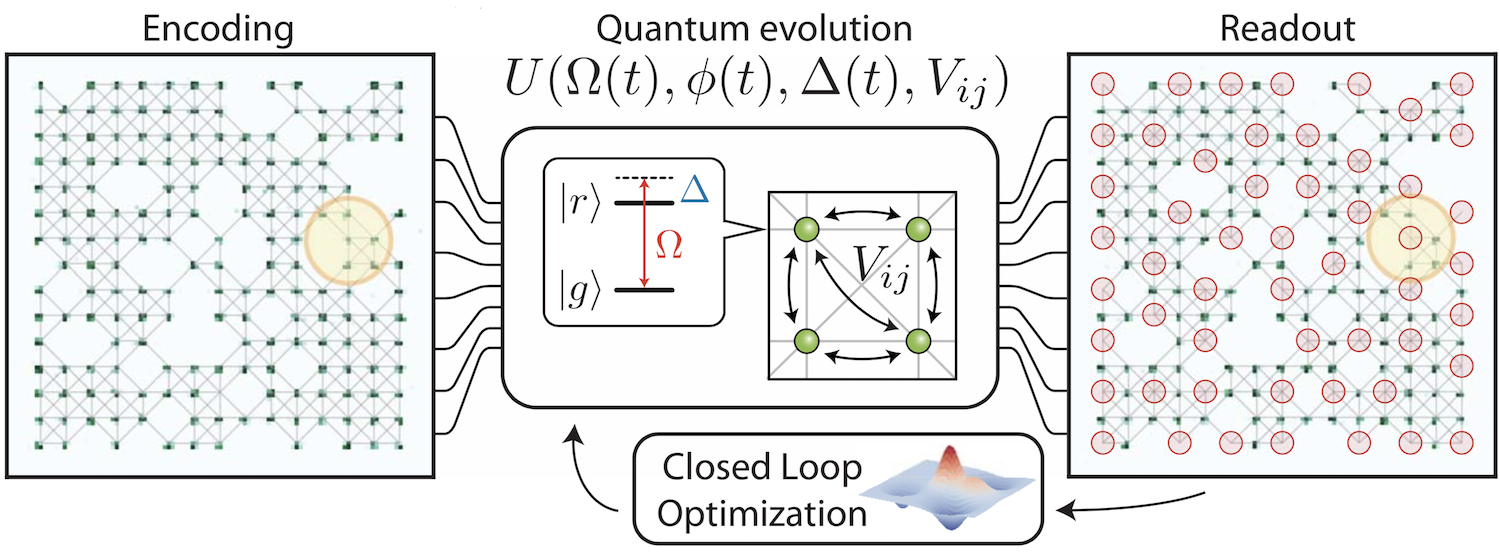Rydberg atom array experiment Although quantum theory promises advantages and speedups for certain applications, implementing them in practice on a real-world quantum device is highly challenging due to imperfections and couplings to environments. To help realize the many promising quantum applications in the laboratory, we work closely with experimentalists (using systems such as Rydberg atoms and superconducting qubits) and push the limits of quantum technology.